理解傅里叶变换

发表于 2022-04-13 分类于控制系统，傅里叶变换阅读次数：阅读次数： Valine：本文字数： 14k

最近学到光栅化时发现完全不理解信号与线性系统中的基础内容🤯.大一高数也没有讲傅里叶变化,于是临时补一下相关定义与推导🤕

p.s. 公式有点多, 可能会出现公式加载失败, 尝试刷新即可

本文分为三个部分介绍傅里叶变换

傅里叶分析直观体验: 来自知乎-傅里叶分析之掐死教程
傅里叶展开与变换的推导: 来自哔哩哔哩-纯干货傅里叶变换
傅里叶应用: 来自哔哩哔哩-现代计算机图形学入门

傅里叶分析直观体验

法国数学家傅里叶认为，任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示

频域与时域

有一段声波, 我们可以将其表示为一段声波曲线

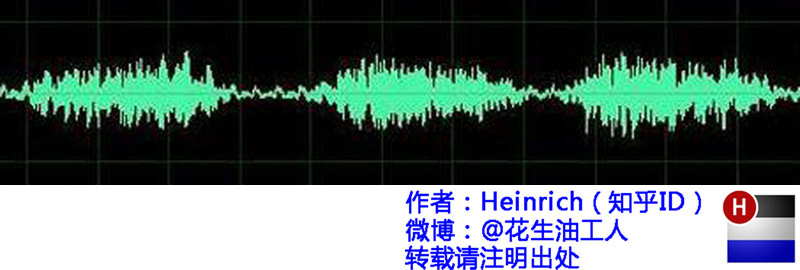
这是一个时间与声波的函数曲线, 我们将其称之为声音的时域表达. 然而, 我们没法从声音中获得更多的信息(如他们是由那些音符合成的?), 我们希望用音符的方式表达音乐(比如/duo/是在那些时候发出的, /ruai/是在什么时候发出的?), 有了这些信息, 我们就可以合成这段声波, 这称为声波的频域表达

前面声波的例子中横轴是时间, 我们可以很轻松的将其理解为时域表达, 对于普通函数图像, 我们也可以将其理解成时域表达. 例如, 下面是一个方波

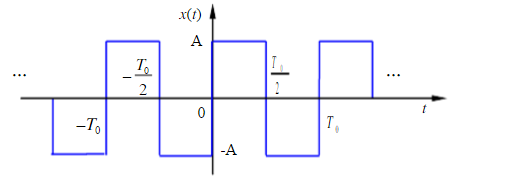
我们可以认为其是方波的时域表达, 同时, 我们可以用无穷个三角函数的和逼近他

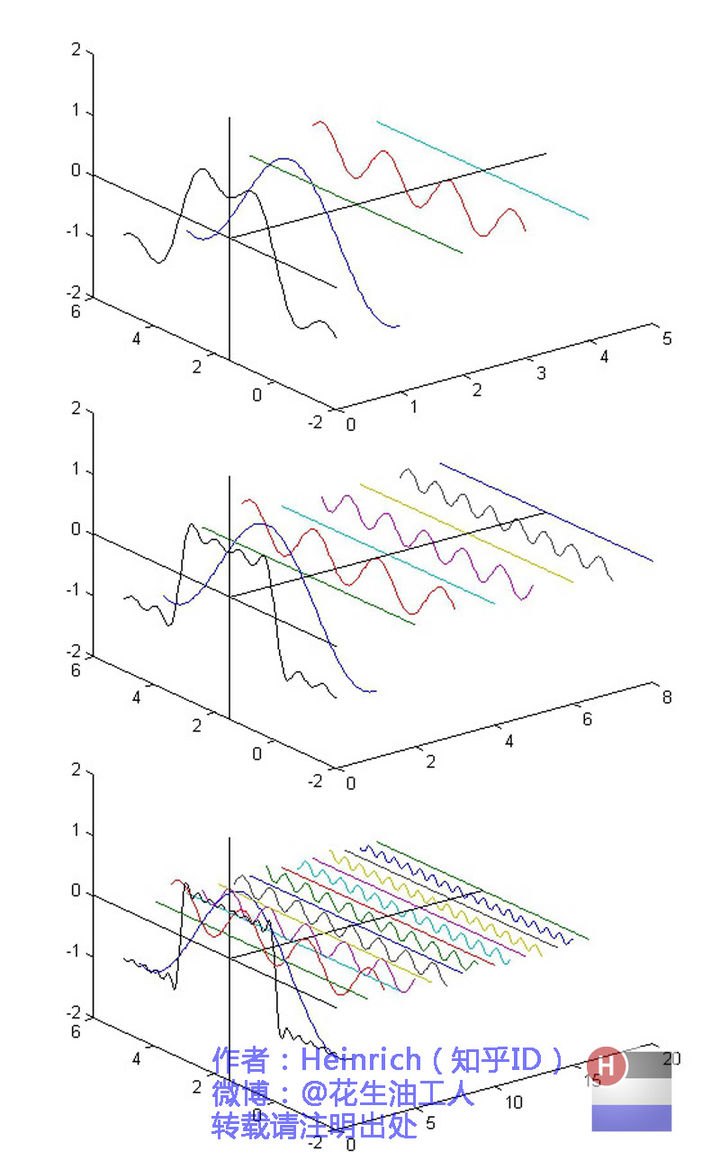
最前面黑色的线就是所有正弦波叠加而成的总和，也就是越来越接近矩形波的那个图形。而后面依不同颜色排列而成的正弦波就是组合为矩形波的各个分量, 其频域表达如下

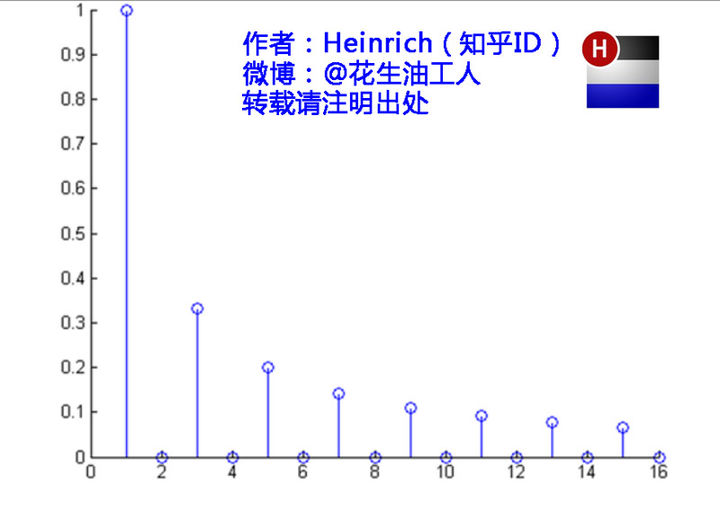
看起来比较奇怪, 实际上, 他就是从侧面看图

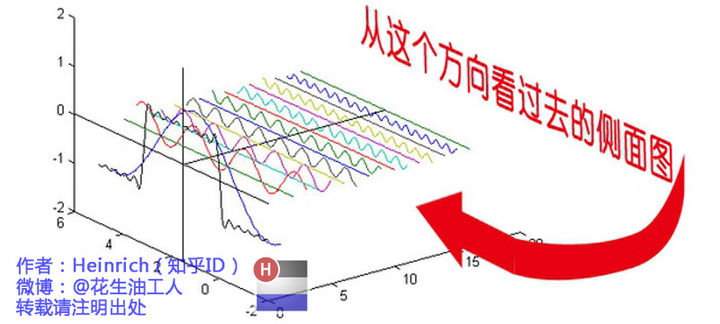
更加完整的表示

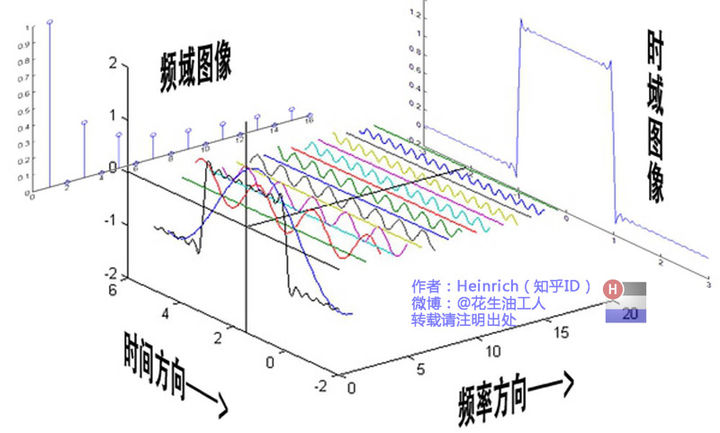
我们也将频域表示图称为时域的频谱

相位谱

在前面, 我们使用三角函数累加逼近一个函数, 一个描述三角函数需要描述其频率, 震幅, 相位. 频率就是频谱的横坐标, 震幅可以用频谱的纵坐标表示, 但是我们没办法表示相位. 所以还需要补充一个相位谱

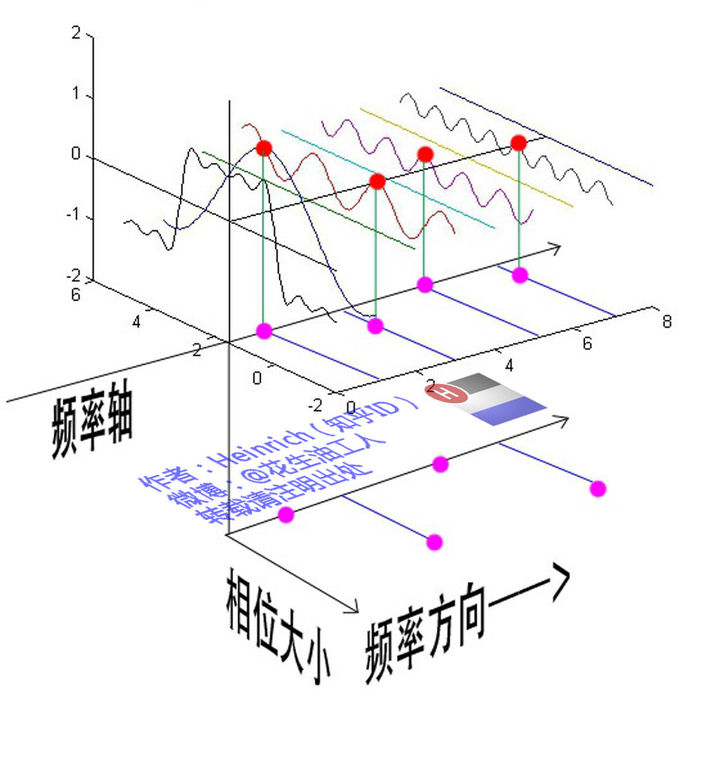
先找出波峰到频率轴的水平距离, 在用这个值除以周期, 就得到了相位大学

傅里叶级数到傅里叶变换

傅里叶认为可以用无穷个频率依次上升的三角函数的无穷级数贴近一个函数, 就像下面这样

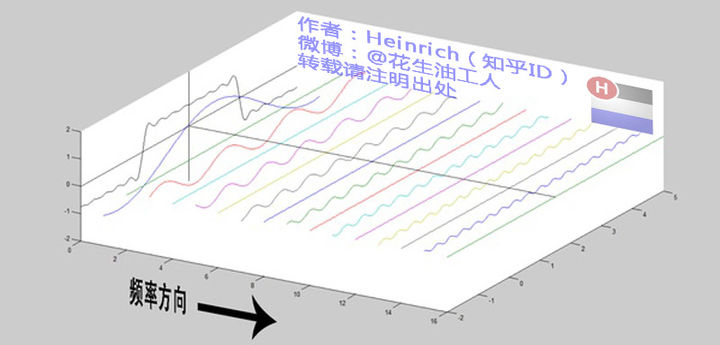
如果忽略级数, 将频率之间的差值变小呢? 从累加$\sum_{n=0}^{\infty}f_n(x)$变成了$\int_0^{\infty}f_\omega(x)d\omega$

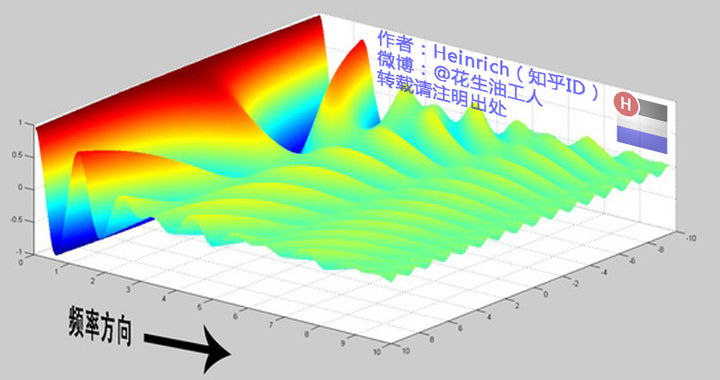
这就是从傅里叶级数到傅里叶变换的过程

傅里叶变换就是将时域表示转换为频域表示. 逆傅里叶变换就是将频域表示转换为时域表示

将三角函数表示在频谱上

频谱看起来很好画, 比如上图, 从侧面观测一下, 我们就可以得到频谱, 但是有个小问题, 在级数那里, 我们还可以看到三角函数之间夹着的的彩色直线, 那些也是参与累加的三角函数, 波浪的是$\cos$函数, 直线是$\sin$函数, 只不过$\omega = 0$, 所以表达成了直线, 我们如何用一个数同时表达$\cos$与$\sin$的频率呢? 借用复平面与欧拉公式

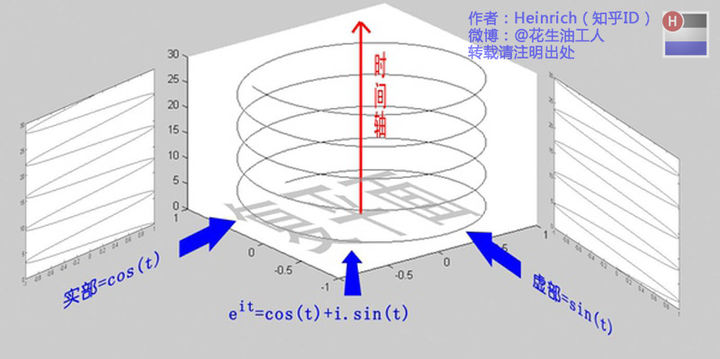
最后得到傅里叶变换频谱

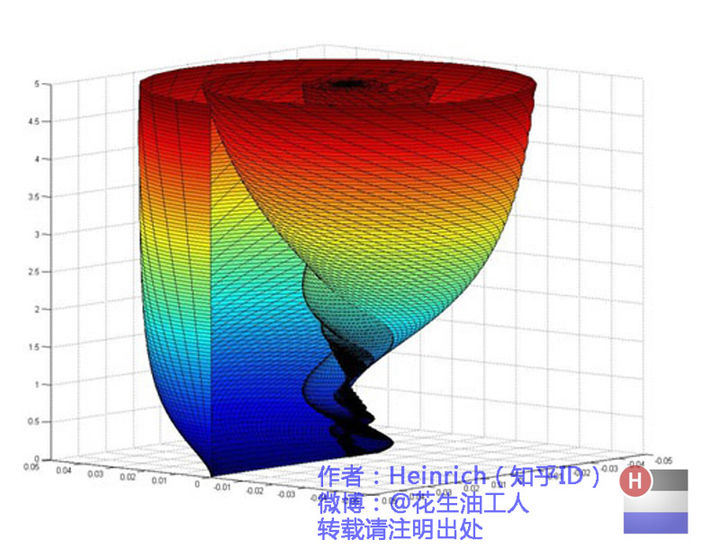
傅里叶变换推导

三角函数正交性

三角函数系定义如下:
\[ \{ 1, \sin x, \cos x, \ldots, \sin nx, \cos nx, \ldots , \sin mx, \cos mx, \ldots \} \]
在这里, 可以将$1$看作是$\cos 0x$, 还可以为三角函数系加上一个元素$0$(即$\sin 0x$)
正交函数定义如下:
若$f(x)$, $g(x)$在区间$[a,b]$上有定义, 且 \[ \int_a^b f(t)g(t)dt = 0 \] 那么就说$f(x), g(x)$在区间$[a,b]$上正交
三角函数系的正交性: 任意两个三角函数系的函数($m\neq n$)的积在区间长度为$2\pi$的区间上内积分为$0$, 证明如下:
首选选取积分范围为$[-\pi, \pi]$(其他区间可以由周期函数性质推得)
- 若选取$f(x) = \sin nx$, $g(x) = \cos mx$, 积分为 \[ \int_{-\pi}^\pi \sin nx \ \cos mx \ dx \] 由奇函数性质可知积分为$0$
- 若选取$f(x) = \cos nx$, $g(x) = \cos mx$, 积分为 \[ \int_{-\pi}^\pi \cos nx \ \cos mx \ dx \] 由积化和差公式
  \[ \cos \alpha \ \cos \beta = \frac{1}{2}[\cos(\alpha+\beta)+\cos(\alpha-\beta)] \]
  知,
  - 当$m \neq n$时: \[ \begin{align} & \int_{-\pi}^\pi \cos nx \ \cos mx \ dx \\ = & \int_{-\pi}^\pi \frac{1}{2} [ \cos (n+m) x + \cos (n-m) x ] \ dx \\ = & \frac{1}{2}\left[\int_{-\pi}^\pi \cos (n+m)x \ dx+ \int_{-\pi}^\pi \cos (n-m)x \ dx \right]\\ = & \frac{1}{2}\left[\left. \frac{1}{m+n} \sin (n+m)x \right|_{-\pi}^\pi + \left. \frac{1}{m-n} \sin (n-m)x \right|_{-\pi}^\pi\right]\\ = & 0 \end{align} \]
  - 顺便看一下当$m = n$时: \[ \begin{align} & \int_{-\pi}^\pi \cos nx \ \cos mx \ dx \\ = & \int_{-\pi}^\pi \frac{1}{2} [ \cos 2n x + \cos 0 x ] \ dx \\ = & \frac{1}{2}\int_{-\pi}^\pi cos 2nx \ dx + \pi \\ = & 0 + \pi \\ = & \pi \end{align} \]
- 若选取$f(x) = \sin nx$, $g(x) = \sin mx$, 积分为
  \[ \int_{-\pi}^\pi \sin nx \ \sin mx \ dx \] 由积化和差公式
  \[ \sin \alpha \ \sin \beta = -\frac{1}{2}[\cos(\alpha+\beta)-\cos(\alpha-\beta)] \]
  知,
  - 当$m \neq n$时: \[ \begin{align} & \int_{-\pi}^\pi \sin nx \ \sin mx \ dx \\ = & \int_{-\pi}^\pi -\frac{1}{2} [ \cos (n+m) x - \cos (n-m) x ] \ dx \\ = & -\frac{1}{2}\left[\int_{-\pi}^\pi \cos (n+m)x \ dx- \int_{-\pi}^\pi \cos (n-m)x \ dx \right]\\ = & - \frac{1}{2}\left[\left. \frac{1}{m+n} \sin (n+m)x \right|_{-\pi}^\pi - \left. \frac{1}{m-n} \sin (n-m)x \right|_{-\pi}^\pi\right]\\ = & 0 \end{align} \]
  - 顺便看一下当$m = n$时: \[ \begin{align} & \int_{-\pi}^\pi \sin nx \ \sin mx \ dx \\ = & \int_{-\pi}^\pi -\frac{1}{2} [ \cos 2n x - \cos 0 x ] \ dx \\ = & -\frac{1}{2}\int_{-\pi}^\pi cos 2nx \ dx +\pi \\ = & 0 + \pi \\ = & \pi \end{align} \]
至此, 证明了三角函数正交性

周期为$2\pi$函数的傅里叶展开

假设$f(x) = f(x+2\pi)$, 傅里叶级数可以理解为: 周期为$2\pi$的函数可以表示为无限个三角函数的和(具体原因需要参考信号系统课程), 按照这样的思想, 我们写下朴素的表达式

\[ f(x) = \sum_{n=0}^{+\infty} a_n \cos nx + \sum_{n=0}^{+\infty}b_n \sin nx \] 教材上定义

\[ f(x) = \frac{a_0}{2} + \sum_{n=1}^{+\infty} a_n \cos nx + \sum_{n=1}^{+\infty}b_n \sin nx \]

有些出入, 尝试将$n=0$单独拿出来

\[ \begin{align} f(x) & = a_0 \cos 0x + b_0 \sin 0x + \sum_{n=1}^{+\infty} a_n \cos nx + \sum_{n=1}^{+\infty}b_n \sin nx \\ & = a_0 + \sum_{n=1}^{+\infty} a_n \cos nx + \sum_{n=1}^{+\infty}b_n \sin nx \end{align} \] 与教材上的$\frac{a_0}{2}$有些出入, 但是$a_0$是个常数, 形式是什么样式无所谓,

不妨先求出$a_0$
我们发现两个$\sum$中都有一个三角函数, 也可以看作是$\cos 0x \times 三角函数$, 如果对其做一个区间长为$2\pi$的积分, 结果为$0$, 这样就可以消去$a_n$了. \[ \begin{align} \int_{-\pi}^\pi f(x) dx & = \int_{-\pi}^\pi a_0 \ dx + \int_{-\pi}^\pi \sum_{n=1}^{+\infty}a_n \cos nx\ dx + \int_{-\pi}^\pi \sum_{n=1}^{+\infty}b_n \sin nx\ dx \\ \int_{-\pi}^\pi f(x) dx & = \int_{-\pi}^\pi a_0 \ dx + \sum_{n=1}^{+\infty} a_n \int_{-\pi}^\pi \cos nx\ dx +\sum_{n=1}^{+\infty}b_n \int_{-\pi}^\pi \sin nx\ dx \\ \int_{-\pi}^\pi f(x) dx & = \int_{-\pi}^\pi a_0 \ dx \\ \int_{-\pi}^\pi f(x) dx & = 2\pi a_0\\ a_0 & = \frac{\int_{-\pi}^\pi f(x) dx}{2 \pi} \end{align} \] 这里的$a_0$就是教材上$\frac{a_0}{2}$, 即教材上的$a_0 = \frac{\int_{-\pi}^\pi f(x) dx}{\pi}$, 教材上使用$\frac{a_0}{2}$表示就是为了形式上的好看, 毕竟$a_0$是个常数
继续求出$a_n$
与求$a_0$思路一样, 我们希望消除所有有$b_n sin\ nx$的项, 将 \[ \begin{align} f(x) = a_0 + \sum_{n=1}^{+\infty} a_n \cos nx + \sum_{n=1}^{+\infty}b_n \sin nx \end{align} \] 的两边同时乘$\cos mx$并在长为$2\pi$的区间上积分, 我们就可以构造出$_{-}^ mx nx $, 根据奇函数性质, 我们知道这一项恒等于$0$(无论$m$是否等于$n$), 于是得出 \[ \begin{align} \int_{-\pi}^\pi f(x) \cos\ mx\ dx & = \int_{-\pi}^\pi a_0\cos\ mx\ dx + \int_{-\pi}^\pi \sum_{n=1}^{+\infty} a_n \cos nx \cos mx\ dx +\int_{-\pi}^\pi \sum_{n=1}^{+\infty}b_n \sin nx \cos\ mx\ dx \\ \int_{-\pi}^\pi f(x) \cos\ mx\ dx & = \int_{-\pi}^\pi a_0\cos\ mx\ dx + \sum_{n=1}^{+\infty} a_n \int_{-\pi}^\pi \cos nx \cos mx\ dx + \sum_{n=1}^{+\infty}b_n \int_{-\pi}^\pi\sin nx \cos\ mx\ dx \\ \int_{-\pi}^\pi f(x) \cos\ mx\ dx & = \int_{-\pi}^\pi a_0\cos\ mx\ dx + \sum_{n=1}^{+\infty} a_n \int_{-\pi}^\pi \cos nx \cos mx\ dx + 0 \\ \end{align} \] 当$n \neq m$时, 根据三角函数正交性, $\int_{-\pi}^\pi \cos nx \cos mx\ dx = 0$, 即 \[ \begin{align} \int_{-\pi}^\pi f(x) \cos\ mx\ dx & = \int_{-\pi}^\pi a_0\cos\ mx\ dx + a_m \int_{-\pi}^\pi \cos mx \cos mx\ dx \\ \end{align} \] 在求三角函数正交性时, 我们推出过$\int_{-\pi}^\pi \cos mx \cos mx\ dx = \pi$, 即 \[ \begin{align} \int_{-\pi}^\pi f(x) \cos\ mx\ dx & = \int_{-\pi}^\pi a_0\cos\ mx\ dx + a_m \pi \\ \end{align} \] 继续简化, 我们知道$m=n$, 而$n\in [1,\infty)$, 即$m\neq 0$ \[ \begin{align} \int_{-\pi}^\pi f(x) \cos\ mx\ dx & = \int_{-\pi}^\pi a_0\cos\ mx\ dx + a_m \pi \\ \int_{-\pi}^\pi f(x) \cos\ mx\ dx & = a_0\int_{-\pi}^\pi \cos\ 0x \cos\ mx\ dx + a_m \pi \\ \int_{-\pi}^\pi f(x) \cos\ mx\ dx & = a_m \pi \\ a_m & = \frac{\int_{-\pi}^\pi f(x) \cos\ mx\ dx }{\pi} \end{align} \] 于是得到 \[ a_n = \frac{\int_{-\pi}^\pi f(x) \cos\ nx\ dx }{\pi} \] 实际上, 在这里我们可以看到, 当$n=0$时, $a_0 = \frac{\int_{-\pi}^\pi f(x) \cos\ 0x\ dx }{\pi}= \frac{\int_{-\pi}^\pi f(x) dx }{\pi}$与教材中$a_0$是一样的, 这就是教材用$\frac{a_0}{2}$形式的原因
继续求出$b_n$
与求$b_n$思路一样, 我们希望消除所有有$a_n \cos\ nx$的项, 将 \[ \begin{align} f(x) = a_0 + \sum_{n=1}^{+\infty} a_n \cos nx + \sum_{n=1}^{+\infty}b_n \sin nx \end{align} \] 的两边同时乘$\sin mx$并在长为$2\pi$的区间上积分, 我们就可以构造出$_{-}^ mx nx $, 根据奇函数性质, 我们知道这一项恒等于$0$(无论$m$是否等于$n$), 于是得出 \[ \begin{align} \int_{-\pi}^\pi f(x) \sin\ mx\ dx & = \int_{-\pi}^\pi a_0\sin\ mx\ dx + \int_{-\pi}^\pi \sum_{n=1}^{+\infty} a_n \cos nx \sin mx\ dx +\int_{-\pi}^\pi \sum_{n=1}^{+\infty}b_n \sin nx \sin\ mx\ dx \\ \int_{-\pi}^\pi f(x) \sin\ mx\ dx & = \int_{-\pi}^\pi a_0\sin\ mx\ dx + \sum_{n=1}^{+\infty} a_n \int_{-\pi}^\pi \cos nx \sin mx\ dx + \sum_{n=1}^{+\infty}b_n \int_{-\pi}^\pi \sin nx \sin\ mx\ dx \\ \int_{-\pi}^\pi f(x) \sin\ mx\ dx & = \int_{-\pi}^\pi a_0\sin\ mx\ dx + \sum_{n=1}^{+\infty} a_n \times 0 + \sum_{n=1}^{+\infty}b_n \int_{-\pi}^\pi \sin nx \sin\ mx\ dx \\ \int_{-\pi}^\pi f(x) \sin\ mx\ dx & = \int_{-\pi}^\pi a_0\sin\ mx\ dx + \sum_{n=1}^{+\infty}b_n \int_{-\pi}^\pi \sin nx \sin\ mx\ dx \\ \end{align} \] 当$n \neq m$时, 根据三角函数正交性, $\int_{-\pi}^\pi \sin nx \sin\ mx\ dx = 0$, 即 \[ \begin{align} \int_{-\pi}^\pi f(x) \sin\ mx\ dx & = \int_{-\pi}^\pi a_0\sin\ mx\ dx + b_m \int_{-\pi}^\pi \sin mx \sin\ mx\ dx \end{align} \] 在求三角函数正交性时, 我们推出过$\int_{-\pi}^\pi \sin mx \sin mx\ dx = \pi$, 即 \[ \begin{align} \int_{-\pi}^\pi f(x) \sin\ mx\ dx & = \int_{-\pi}^\pi a_0\sin\ mx\ dx + b_m \pi \\ \end{align} \] 继续简化, 我们知道$m=n$, 而$n\in [1,\infty)$, 即$m\neq 0$ \[ \begin{align} \int_{-\pi}^\pi f(x) \sin\ mx\ dx & = \int_{-\pi}^\pi a_0\sin\ mx\ dx + b_m \pi \\ \int_{-\pi}^\pi f(x) \sin\ mx\ dx & = a_0\int_{-\pi}^\pi \cos\ 0x\sin\ mx\ dx + b_m \pi \\ \int_{-\pi}^\pi f(x) \sin\ mx\ dx & = b_m \pi \\ b_m = \frac{\int_{-\pi}^\pi f(x) \sin\ mx\ dx}{\pi} \end{align} \] 于是得到 \[ b_n = \frac{\int_{-\pi}^\pi f(x) \sin\ nx\ dx}{\pi} \]

最后得到周期为$2\pi$函数的傅里叶展开 \[ \begin{align} f(x) &= f(x+2\pi)\\ f(x) &= \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos\ nx+ \sum_{n=1}^{\infty} b_n \sin\ nx\\ a_n &= \frac{\int_{-\pi}^\pi f(x) \cos\ nx\ dx }{\pi}\\ b_n &= \frac{\int_{-\pi}^\pi f(x) \sin\ nx\ dx}{\pi}\\ \end{align} \]

周期为$T$函数的傅里叶展开

使用换元将$f(x)$的周期从$2\pi$推广到$T$, 我们需要将三角函数的周期与积分区间长度变成$T$, 即对于三角函数有 \[ \begin{align} \frac{2\pi}{\omega} & = T\\ \omega & = \frac{2\pi}{T}\\ \end{align} \] 选取积分区间$[0,T]$(选哪里都可以, 只要是一个周期就行)对参数变换 \[ \begin{align} \cos x \to \cos \omega x \\ \sin x \to \sin \omega x \\ \end{align} \]

\[ \begin{align} a_n &= \frac{\int_{-\pi}^\pi f(x) \cos\ nx\ dx }{\pi} &\to a_n &= \frac{2\int_0^T f(x) \cos\ n\omega x\ dx }{T} \\ b_n &= \frac{\int_{-\pi}^\pi f(x) \sin\ nx\ dx }{\pi} &\to b_n &= \frac{2\int_0^T f(x) \sin\ n\omega x\ dx }{T} \\ \end{align} \] 得到周期为$T$函数的傅里叶展开 \[ \begin{align} f(x) & = \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos\ n\omega x + \sum_{n=1}^{\infty} b_n \sin\ n\omega x\\ a_n & = \frac{2\int_0^T f(x) \cos\ n\omega x\ dx }{T} \\ b_n & = \frac{2\int_0^T f(x) \sin\ n\omega x\ dx }{T} \\ \omega & = \frac{2\pi}{T} \end{align} \]

傅里叶级数的复数形式

利用欧拉公式

\[ e^{i\theta} = \cos\theta + i\sin\theta \]

令$\theta' = -\theta$我们可以相加减得到 \[ \begin{align} \cos\theta &= \frac{1}{2} (e^{i\theta}+e^{-i\theta})\\ \sin\theta &= -\frac{1}{2}i (e^{i\theta}-e^{-i\theta})\\ \end{align} \] 带入周期为$T$的傅里叶展开 \[ \begin{align} f(x) & = \frac{a_0}{2} + \sum_{n=1}^{\infty} \frac{1}{2}a_n (e^{in\omega x}+e^{-in\omega x}) - \sum_{n=1}^{\infty} \frac{1}{2}ib_n (e^{in\omega x}-e^{-in\omega x}) \\ \end{align} \] 分别将$e^{in\omega t}$与$e^{-in\omega t}$合并 \[ \begin{align} f(x) & = \frac{a_0}{2} + \sum_{n=1}^{\infty} \frac{1}{2}(a_n-ib_n)e^{in\omega x}+\sum_{n=1}^{\infty} \frac{1}{2}(a_n+ib_n)e^{-in\omega x} \end{align} \] 我们发现后两项具有类似的$\frac{1}{2}(a_n?ib_n)e^{?in\omega x}$的结构, 将后半部分的$n$换元为$-n$ \[ \begin{align} f(x) & = \frac{a_0}{2} + \sum_{n=1}^{\infty} \frac{1}{2}(a_n-ib_n)e^{in\omega x}+\sum_{n=-\infty}^{-1} \frac{1}{2}(a_{-n}+ib_{-n})e^{in\omega x} \end{align} \] 尝试将同样的结构应用于$\frac{a_0}{2}$, 于是得到 \[ \frac{a_0}{2} = \sum_{n=0}^{0}\frac{1}{2}(a_0)e^{i0\omega x} \] 形式完全统一了 \[ f(x) = \sum_{-\infty}^{\infty} C_n e^{in\omega x} \\ \]

\[ C_n = \left\{ \begin{align} &\frac{a_0}{2}, & n=0 \\ &\frac{a_n-ib_n}{2}, & n\in(0,+\infty) \cap \mathbb{Z} \\ &\frac{a_{-n}+ib_{-n}}{2}, & n\in(-\infty, 0)\cap \mathbb{Z} \\ \end{align} \right. \] 带入$a_n, b_n$, 得到

对于$C_0$
\[ \begin{align} C_0 & = \frac{a_0}{2} \\ & = \frac{1}{2} \frac{2}{T}\int_0^T f(x) \cos\ 0\omega x\ dx \\ & = \frac{1}{T}\int_0^T f(x)\ dx \\ \end{align} \]
对于$C_n(n\in[0,+\infty) \cap \mathbb{Z})$
\[ \begin{align} C_n & = \frac{a_n-ib_n}{2} \\ & = \frac{1}{2}\frac{2}{T}\left( \int_0^Tf(x)\cos n\omega x \ dx-i \int_0^Tf(x)\sin n\omega x\ dx\right)\\ & = \frac{1}{T} \int_0^Tf(x)\left( \cos n\omega x - i\sin n\omega x\right)\ dx \end{align} \]
结果的括号中很像欧拉公式, 但是虚部前为负号, 由于$\cos x$为偶函数, $\sin x$ 为奇函数 \[ \begin{align} C_n & = \frac{1}{T} \int_0^Tf(x)\left( \cos n\omega x - i\sin n\omega x\right)\ dx\\ & = \frac{1}{T} \int_0^Tf(x)\left( \cos \left(-n\omega x) + i\sin (-n\omega x\right)\right)\ dx\\ & = \frac{1}{T} \int_0^Tf(x)e^{-in\omega x}\ dx \end{align} \]
对于$C_n(n\in(-\infty,0) \cap \mathbb{Z})$
\[ \begin{align} C_n & = \frac{a_{-n}+ib_{-n}}{2} \\ & = \frac{1}{2}\frac{2}{T}\left( \int_0^Tf(x)\cos (-n\omega x)\ dx+i \int_0^Tf(x)\sin (-n\omega x)\ dx \right)\\ & = \frac{1}{T} \int_0^Tf(x)\left( \cos n\omega x - i\sin n\omega x\right) dx \\ & = \frac{1}{T} \int_0^Tf(x)e^{-in\omega x}\ dx \end{align} \]

发现$C_n(n\in(-\infty,0) \cap \mathbb{Z})$与$C_n(n\in(0,+\infty) \cap \mathbb{Z})$的表达式是一样的, 同时将$n=0$代入$C_n(n\in(-\infty,0) \cap \mathbb{Z})$表达式, 发现结果与$C_0$相同, 最后$C_n$被统一为 \[ C_n = \frac{1}{T} \int_0^Tf(x)e^{-in\omega x}\ dx \] 即 \[ \begin{align} f(x) &= f(x+T) \\ f(x) &= \sum_{-\infty}^{\infty}C_ne^{in\omega x}\\ C_n &= \frac{1}{T} \int_0^Tf(x)e^{-in\omega x}\ dx\\ \end{align} \]

傅里叶变换

希望将非周期函数$f(x)$表示为傅里叶展开, \[ \begin{align} f(x) &= \sum_{-\infty}^{\infty}C_ne^{in\omega x}\\ C_n &= \frac{1}{T} \int_0^Tf(x)e^{-in\omega x}\ dx\\ \end{align} \] 可以发现$e^{in\omega x}$是一个固定模式, $f(x)$展开后的每一项都是由$C_n$决定的, $C_n$是一个复数, 可以将$C_n$取值画在一个复平面上, 将不同$n\omega$下的$C_n$画在一个三维坐标系上($n\omega-C_n$), 即我们得到了$f(x)$的频域表达

可以把非周期函数当作$T\to +\infty$的周期函数, 此时频谱上的$w$之间距离$\Delta w\to0$, $f(x)$的频谱上的离散点变连续, 成为连续函数, 此时, 我们就可以将$\sum^\infty_{n=-\infty}\Delta\omega$变为$\int_{-\infty}^{\infty} d\omega$

将$C_n$代入$f(x)$ \[ f(x) = \sum_{-\infty}^{\infty} \frac{1}{T} \int_0^Tf(x)e^{-in\omega x}\ dx e^{in\omega x}\\ \] 出了个小问题, 我们找不前面说的$\Delta\omega$了...但是, 有 \[ \frac{\omega}{2\pi} = \frac{1}{T}\\ \] 代入得到 \[ \begin{align} f(x) &= \sum_{-\infty}^{\infty} \frac{1}{T} \int_0^Tf(x)e^{-in\omega x}\ dx e^{in\omega x}\\ &=\frac{1}{2\pi}\sum_{-\infty}^{\infty} \int_0^T \omega f(x)e^{-in\omega x}\ dx e^{in\omega x}\\ \end{align} \] 将$C_n$的积分区间从$[0,T]$换到$[-\frac{T}{2}, \frac{T}{2}]$(这个积分区间是可以随便换的, 只要区间长为T就行, 在前面推导过程中也没有利用到$[0,T]$的特殊性质) \[ f(x) =\frac{1}{2\pi}\sum_{n=-\infty}^{\infty} \int_{-\frac{T}{2}}^{\frac{T}{2}} \omega f(x)e^{-in\omega x}\ dx e^{in\omega x} \] 我们又有$\Delta\omega\to 0, T\to +\infty$ \[ \begin{align} f(x)&=\frac{1}{2\pi}\int_{-\infty}^{+\infty} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x)e^{-i\omega x}\ dx e^{i\omega x}\ d\omega\\ &=\frac{1}{2\pi}\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x)e^{-i\omega x}\ dx e^{i\omega x}\ d\omega\\ \end{align} \]

注意, 指数上的$n\omega$变成了$\omega$, 因为我们将加和变成了积分

将时域到频域的变换 \[ F(w) = \int_{-\infty}^{+\infty} f(x)e^{-in\omega x}\ dx \]
称为傅里叶变换
将频域到是时域的变换 \[ \begin{align} f(x)&=\frac{1}{2\pi}\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x)e^{-in\omega x}\ dx e^{in\omega x}\ d\omega\\ &=\frac{1}{2\pi}\int_{-\infty}^{+\infty} F(w) e^{in\omega x}\ d\omega \end{align} \]
称为逆傅里叶变换

最后想想我们做了什么

证明了三角函数正交性, 求了$\int_{0}^{\pi} \sin nx \sin nx\ dx = \int_{0}^{\pi} \cos nx \cos nx\ dx = \pi$
利用三角函数正交性求出了周期为$2\pi$函数的傅里叶展开
将周期从$2\pi$推广到$T$, 得到了傅里叶展开的一般形式
利用欧拉公式替换傅里叶展开中的三角函数, 合并, 换元, 得到傅里叶展开的复数表现形式
将非周期函数转为周期无穷大的周期函数, 将加和转为积分, 最终得到傅里叶变换与逆变换. 利用频域表达解释了积分的合理性

傅里叶变换应用

傅里叶变换最大的应用就是滤波, 我们可以利用傅里叶变换将时域表达转换为频域表达, 然后手动移除一些无用的频率, 最终通过逆傅里叶变换得到滤波后时域表达. 在图形学中, 我们可以认为图像是图的时域表达, 并获取其频域表达图

左边是时域, 右边是频域. 在频谱中, 光亮越靠近中心, 频率越低. 大部分图像的频谱主要都集中在低频. 我们还可以看到水平与垂直的两条光亮, 这是因为在傅里叶变换时, 我们将图像的左右两边, 上下两边连了起来, 使之成为了一个无限大的图像, 而左右边缘, 上边缘差异就很大, 于是频率很高, 出现了两个亮条.

高频一般代表这图形的边界(色彩变化很明显), 而低频一般代表非边界(因为色彩变化不明显)

我们使用一个低通滤波器过滤掉高频波, 效果如下

图像边界没了, 图像变得模糊了, 还可以应用一个高通滤波器, 效果如下

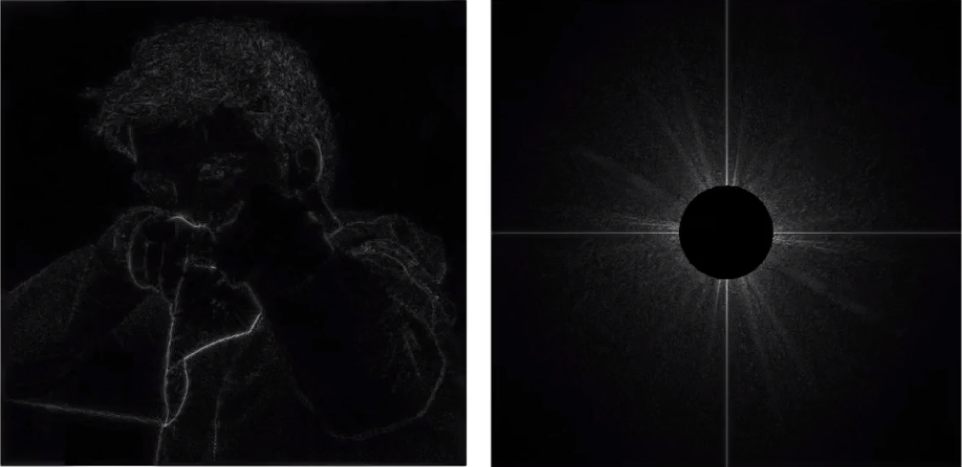
只有边界信息被保留了下来...