2020牛客寒假算法基础集训营6题解

发表于 分类于 ， 阅读次数： 阅读次数： Valine： 本文字数： 8.8k
原题来自2020牛客寒假算法基础集训营6，作以存档备查

A: 配对

在这里插入图片描述 输入

3 2
1 2 3
1 2 3

输出

5

考虑贪心：首先，用A中最大的K个数字和B中最大的K个数字去组合如果A1<A2,B1<B2，那么一定是由A1和B2配对较优。所以，倒序配对是最优的

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

int a[100050],b[100050];

bool cmp(int a,int b){
    return a>b;
}

int main(){
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++)scanf("%d",&a[i]);
    for(int i=0;i<n;i++)scanf("%d",&b[i]);
    sort(a,a+n,cmp);
    sort(b,b+n,cmp);
    sort(a,a+k);
    int ans=0x3f3f3f3f;
    for(int i=0;i<k;i++)ans=min(ans,a[i]+b[i]);
    cout<<ans;
    return 0;
}

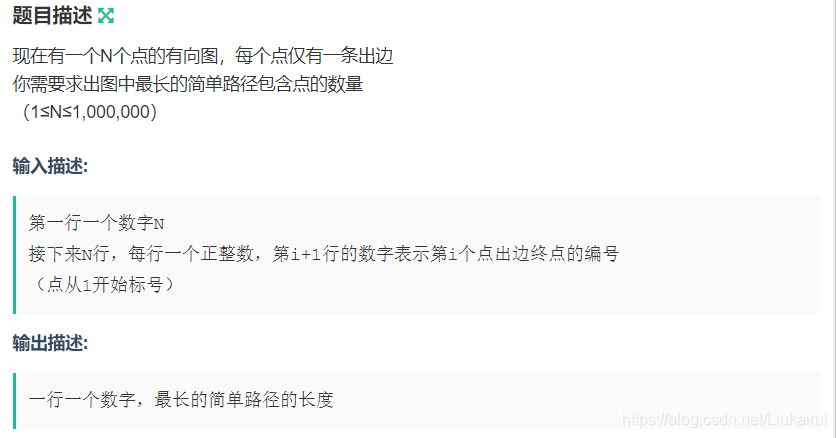
B: 图

在这里插入图片描述 输入

3
2
3
2

输出

3

n-1条边也就是说他是一棵树，所以这个题相当于是在问图的直径，见文章：关于计蒜客习题：网络延迟的思路（求树的最大直径求法与证明）

#include<bits/stdc++.h>
using namespace std;

int n,to[1000050],dp[1000050],deep[1000050];
bool vis[1000050];

void dfs(int pos,int dep){
    vis[pos]=1;deep[pos]=dep;
    if(dp[to[pos]])dp[pos]=dp[to[pos]]+1;
    else if(deep[to[pos]]){
        dp[pos]=(deep[pos]-deep[to[pos]]+1);
        int nw=to[pos];
        while(nw!=pos){
            dp[nw]=dp[pos];
            nw=to[nw];
        }
    }
    else {
        dfs(to[pos],dep+1);
        if(!dp[pos])dp[pos]=dp[to[pos]]+1;
    }
}

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d",&to[i]);
    for(int i=1;i<=n;i++)if(!vis[i])dfs(i,0);
    int ans=0;
    for(int i=1;i<=n;i++)ans=max(dp[i],ans);
    cout<<ans;
    return 0;
}

C: 汉诺塔

在这里插入图片描述 输入

3
1 1
2 3
3 2

输出

2
1 1 2

官方题解： 将木板按照Xi从小到大排序，将这时的Yi数列记为Zi数列，则问题变成将Zi划分为尽可能少的若干组上升子序列。 根据Dilworth定理，最小组数等于Zi的最长下降子序列长度。 要求最长下降子序列的长度，我们有一种经典的二分优化dp的方法，在这里不再详述。 借助这种做法我们能给出一种构造方法，在求出最小组数的同时得出方案。 将状态数组的每个位置变为栈，用入栈操作代替修改元素操作，即可在求出组数的同时，用这些栈来完成对数列的划分。

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5,INF=1e9;
int d[maxn],bl[maxn];
struct node{
   int x,y,id;
   bool operator < (const node &rhs) const{
      return x<rhs.x;
   }
}a[maxn];
int main(){
   int n; scanf("%d",&n);
   for(int i=1;i<=n;i++){
      scanf("%d%d",&a[i].x,&a[i].y);
      a[i].id=i;
   }
   sort(a+1,a+n+1);
   int ans=0;
   for(int i=1;i<=n;i++){
      d[i]=-INF;
      int k=lower_bound(d+1,d+i+1,a[i].y,greater<int>())-d;
      ans=max(ans,k),d[k]=a[i].y,bl[a[i].id]=k;
   }
   printf("%d\n%d",ans,bl[1]);
   for(int i=2;i<=n;i++) printf(" %d",bl[i]); puts("");
   return 0;
}

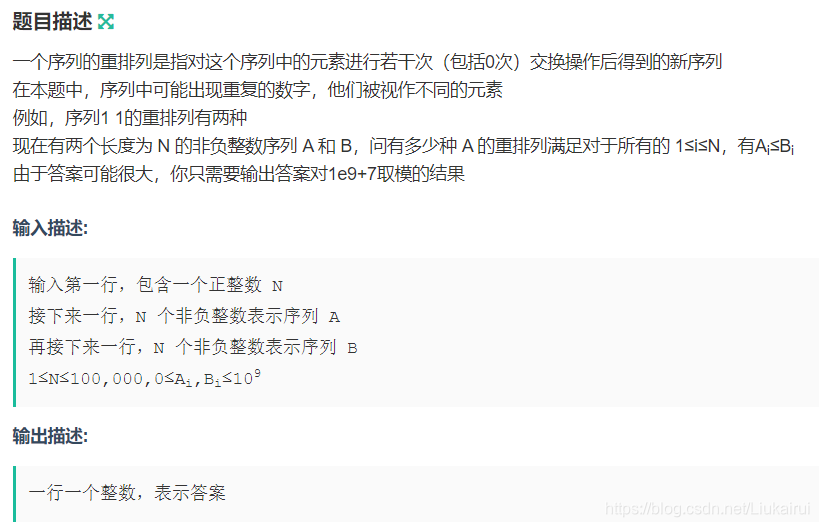
D: 重排列

在这里插入图片描述 输入

4
1 1 2 3
1 2 3 4

输出

8

首先对于输入排序，然后每一个数找到那个比他大的，运用乘法原理即可求解，具体忘了qwq 官方题解是：

容易知道按升序将A和B排序不影响结果。 按标号从小到大考虑A的每个位置填什么数。 例：A（1,2,3）；B（1,3,4） 则考虑第一个位置时，只能填1。 考虑第二个位置时，可以填2或3。 但是由于2和3在这里是完全等价的，也就是说我们并不关心填了谁。 那么我们只需要记录每一步有多少个数可填就好了，这个答案与之前填入的方案无关。 具体实现的时候只需要用双指针进行一轮扫描就可以了。

似乎我不是这样写的...

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

long long ans=1,mod=1000000007,n,a[100050],b[100050];

int main(){
    scanf("%lld",&n);
    for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
    for(int i=1;i<=n;i++)scanf("%lld",&b[i]);
    sort(a+1,a+n+1);
    sort(b+1,b+n+1);
    for(int i=1;i<=n;i++){
        // cout<<((upper_bound(a+1,a+n+1,b[i])-a-i)*ans)%mod<<"  **  ";
        ans=(((upper_bound(a+1,a+n+1,b[i])-a-i+mod)%mod)*ans)%mod;
    }
    if(ans==1)cout<<'0';
    else cout<<ans;
    return 0;
}

E: 立方数

在这里插入图片描述 输入

4
27 24 7 54

输出

3
2
1
3

首先想到的思路是，把这个数的因数搞出来，对于所有的因数，如果(计数>3)就给ans乘上(计数/3). 轻松写出代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <map>
#define ll long long
using namespace std;

map< long, long > mp;

int main(){
    ll t;
    scanf("%lld",&t);
    while(t--){
        mp.clear();
        ll n;
        scanf("%lld",&n);
        for(ll i = 2;i <= n;i++){
            while(n%i == 0){
                if(!mp.count(i))mp[i] = 0;
                ++mp[i];
                n/=i;
            }
        }
        ll ans=1;
        for(auto it = mp.rbegin();it != mp.rend();it++){
            if(it->second >= 3)ans*=it->first * (it->second/3);
        }
        printf("%lld\n",ans);
    }
    return 0;
}

然后轻松TLE，然后我们进行优化，我们枚举每个数的因数，当然是质数，那么枚举范围是0 ~ n吗，不是，是0 ~ n^(1/3) ，因为他要立方 我们继续考虑优化，实际上只需要枚举 0 ~ n^(1/4) 以内的质数去试除，最后剩的数为X 此时X要么是一个完全立方数，要么对答案没有任何贡献，只需要验证X是不是一个完全立方数即可 我们使用二分法确定

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#define ll long long
using namespace std;

const double esp=1e-6;
const int MAX_N=1e5;
int vst[MAX_N],len,p[MAX_N];

int main(){
    for(int i=2;i<=MAX_N;i++){
        if(vst[i]==0){
            p[len++]=i;
            for(int j=2*i;j<MAX_N;j+=i)
                vst[j]=1;
        }
    }
    ll t,n;
    scanf("%lld",&t);
    while(t--){
        ll ans=1;
        scanf("%lld",&n);
        ll max_len=ceil(sqrt(ceil(sqrt(n))));
        for(int i=0;i<len;i++){
            if(p[i]>max_len)break;
            int cnt=0;
            while(n%p[i]==0){
                cnt++;
                n/=p[i];
                if(cnt==3){ans*=p[i];cnt=0;}
            }
        }
        int  l=1,r=1e6;
        while(l<=r){
            ll mid=l+r>>1;
            if(mid*mid*mid==n){
                ans*=mid;
                break;
            }
            else if(mid*mid*mid<n){
                l=mid+1;
            }
            else r=mid-1;
        }
        cout<<ans<<endl;
    }
    return 0;
}

实际上不需要用二分

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 31644;
bool vis[maxn];
vector<ll> pri;
int main(){
    for(int i=2;i<maxn;i++){
        if(!vis[i]){
            pri.push_back(i);
            for(int j=i*i;j<maxn;j+=i){
                vis[j]=1;
            }
        }
    }
    int T;scanf("%d",&T);
    while(T--){
        ll n;scanf("%lld",&n);
        ll ans=1;
        for(int i=0;i<pri.size();i++){
            if(n%pri[i]==0){
                int cnt=0;
                while(n%(pri[i]*pri[i]*pri[i])==0){
                    n/=(pri[i]*pri[i]*pri[i]);cnt++;
                }
                while(n%pri[i]==0) n/=pri[i];
                while(cnt--){
                    ans*=pri[i];
                }
            }
        }
        ll x=pow(n,1.0/3);
        for(ll i=max(1ll,x+1);i<=x+1;i++){
            if(i*i*i==n){
                ans*=i;break;
            }
        }
        printf("%lld\n",ans);
    }
}

F: 十字阵列

在这里插入图片描述 输入

5 5 5
1 1 1
2 2 2
3 3 3
4 4 4
5 5 5

输出

890

说明

造成伤害的情况是：
1 3 4 5 6
3 2 5 6 7
4 5 3 7 8
5 6 7 4 9
6 7 8 9 5

补充的说明：

890 = 1*(1+1)+3*(1+2)+4*(1+3)+...+5*(5+5）,一共25项累加得到890

统计每行每列的总伤害，然后在每次消除的时候删除行列和然后加上交叉点值，不要爆long long

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

long long mod=1000000007;
long long num_c[2050],num_r[2050],h,n,m,ans=0,ex[2050][2050];

int main(){
    scanf("%lld%lld%lld",&n,&m,&h);
    for(int i=0;i<h;i++){
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        num_c[y]+=z;num_r[x]+=z;ex[x][y]+=z;
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            long long tmp=(((num_c[j]+num_r[i]%mod)-ex[i][j])%mod)*(i+j%mod)%mod;
            ans=(ans+tmp)%mod;
        }
    }
    printf("%lld",ans);
    return 0;
}

G: 括号序列

在这里插入图片描述 输入

2
6
())(()
9
()(()()))

输出

2
1

思路与2020寒假训练营第四场B题一样，遇到有问题的就修正然后ans加一即可

#include <iostream>
#include <cstdio>
#include <cstring>
#include <stack>
using namespace std;

stack<char>s;
int t,n;
char ss[1000050];

int main(){
    scanf("%d",&t);
    while(t--){
        int ans=0;
        scanf("%d%s",&n,ss);
        for(int i=0;i<n;i++){
            if(ss[i]=='('||ss[i]=='['||ss[i]=='{')s.push(ss[i]);
            else{
                // cout<<i<<" "<<ss[i]<<" "<<s.size()<<endl;
                if(s.empty()){ans++;}
                else{
                    char tmp=s.top();
                    if((tmp=='{'&&ss[i]=='}')||(tmp=='('&&ss[i]==')')||(tmp=='['&&ss[i]==']'))s.pop();
                    else {ans++;}
                }
            }
        }
        ans+=s.size();
        printf("%d\n",ans);
        while(!s.empty())s.pop();
    }
    return 0;
}

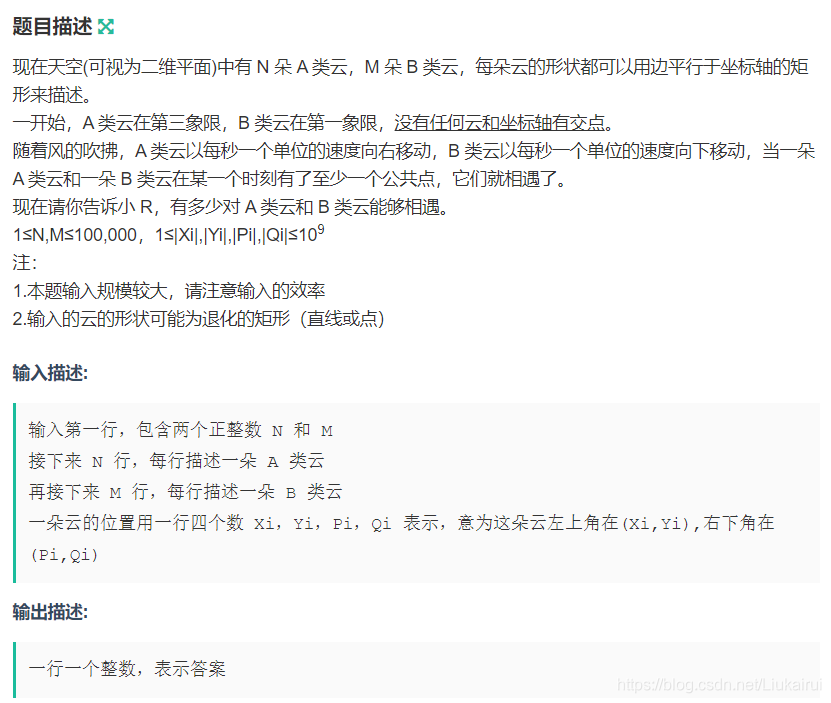
H: 云

在这里插入图片描述 输入

1 1
-2 -1 -1 -2
1 2 2 1

输出

1

官方题解: 直接考虑问题较难，因为两种云都在运动。 但是我们可以考虑相对运动，将这个过程等效为左下角的云朝右上方移动。 在这个背景下我们容易发现：将所有的云投影成y=-x这条直线上的一条线段，则两朵云会相遇当且仅当他们的投影有交点。 这是一个简单的扫描线问题，将线段拆成端点后排序统计即可。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;
typedef long long LL;
const int N = 400050;

struct node{
    int loc, lr, typ;
    inline bool operator < (const node &b)const{
        if(loc == b.loc && lr == b.lr)
            return typ < b.typ;
        if(loc == b.loc)
            return lr > b.lr;
        return loc < b.loc;
    }
}A[N];
int n, m, a, b, c, d, k;
LL cnt[2], ans;

int main()
{

    for(scanf("%d%d", &n, &m); n --;){
        scanf("%d%d%d%d", &a, &b, &c, &d);
        A[++ k] = (node){d - c, 1, 0};
        A[++ k] = (node){b - a, -1, 0};
    }
    while(m --){
        scanf("%d%d%d%d", &a, &b, &c, &d);
        A[++ k] = (node){d - c, 1, 1};
        A[++ k] = (node){b - a, -1, 1};
    }
    sort(A + 1, A + k + 1);
    for(int i = 1; i <= k; i ++){
        cnt[A[i].typ] += A[i].lr;
        if(A[i].lr == 1)
            ans += cnt[A[i].typ ^ 1];
    }
    printf("%lld\n", ans);

    return 0;
}

I: 导航系统

在这里插入图片描述 输入

3
0 1 2
1 0 1
2 1 0
输出

Yes
1
1

输入

3
0 1 1
1 0 1
1 1 0

输出

No

显然数据给出的原图是一棵树。 容易发现，如果将输入的N(N-1)个距离看做N(N-1)条无向边的话，那么如果数据合法，原树就是这张新图的最小生成树。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int MAX_N=550;
const int inf = 0x3f3f3f3f;
int g[MAX_N][MAX_N],n;  // 算法中的 G 矩阵
int rd[3*MAX_N];

bool floyd() {
    for (int k = 0; k < n; ++k) {
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (g[i][k] + g[k][j] != g[i][j]) {
                    return false;
                }
            }
        }
    }
    return true;
}

int main(){
    scanf("%d",&n);
    int cnt=0;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            scanf("%d",&g[i][j]);
            if(g[i][j]!=0)rd[cnt++]=g[i][j];
        }
    }
    if(!floyd())cout<<"No";
    else{
        cout<<"Yes"<<endl;
        sort(rd,rd+cnt);
        for(int i=0;i<2*(n-1);i+=2)cout<<rd[i]<<endl;
    }
    return 0;
}

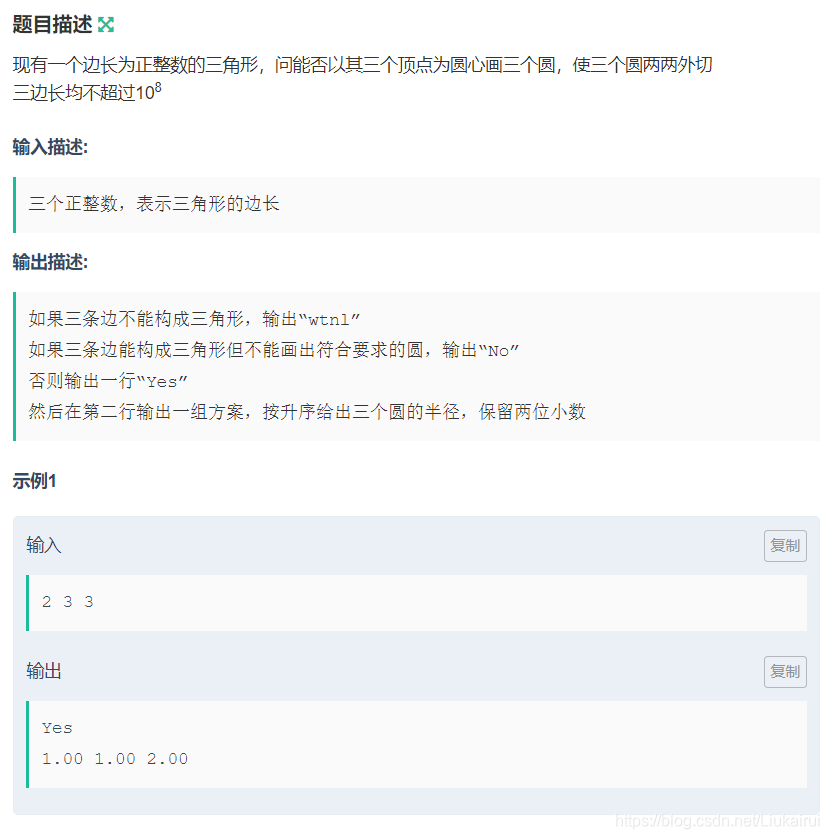
J: 签到题

在这里插入图片描述 输入

2 3 3

输出

Yes
1.00 1.00 2.00

直接列三元一次方程组 设三个圆半径为\(r_1,r_2,r_3\) \[ \begin{cases} r_1+r_2+r_2+r_3>r_1+r_3 \\ r_2+r_3+r_3+r_1>r_1+r_2 \\ r_3+r_1+r_1+r_2>r_2+r_3 \end{cases} \] 求解即可

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

double ans[10];

int main(){
    double a,b,c;
    cin>>a>>b>>c;
    ans[0]=(a+b+c)*0.5-a;
    ans[1]=(a+b+c)*0.5-c;
    ans[2]=(a+b+c)*0.5-b;
    sort(ans,ans+3);
    if(a+b<=c){cout<<"wtnl";return 0;}
    if(ans[0]<=0){cout<<"No";return 0;}
    cout<<"Yes"<<endl;
    for(int i=0;i<3;i++)printf("%.2f ",ans[i]);
    return 0;
}