2020牛客寒假算法基础集训营2题解
A：做游戏
输入
114514 0 0
0 114514 0输出
114514对于三种情况，取每次分组的最小值即可
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int main(){
long long a,b,c,d,e,f;
cin>>a>>b>>c>>d>>e>>f;
cout<<min(a,e)+min(b,f)+min(c,d);
}B：排数字
输入
11
11451419266输出
1计算6,1出现次数即可
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int n;
char ss[200050];
int main(){
scanf("%d",&n);
scanf("%s",ss);
int num_1=0,num_6=0;
for(int i=0;i<n;i++){
if(ss[i]=='1')num_1++;
if(ss[i]=='6')num_6++;
}
if(num_6<=1||num_1==0)cout<<0;
else cout<<min(num_6-1,num_1);
return 0;
}C：算概率
输入
1
500000004输出
500000004 500000004- 考虑dp: dp[i][j]为前i个题答对j个 \(dp[i][j] =(dp[i-1][j-1]*p[i] + dp[i-1][j]*(1-p[i]))\)
- 考虑概率的计算： 分数取模： 方法有很多如计算分子*分母的逆元，... 这里他直接给了取模后的结果，根据同余运算性质直接把他当做概率即可
#include <cstring> #include <iostream> #include <algorithm> using namespace std; const int mod =1e9+7; long long p[2009],dp[2009][2009],n; int main(){ cin >> n ; for(int i=1;i<=n;i++) cin>>p[i]; dp[0][0] =1; for(int i=1 ;i<=n;i++){ dp[i][0] = dp[i-1][0]*(1-p[i])%mod; for(int j=1;j<=i;j++) dp[i][j] =(dp[i-1][j-1]*p[i] + dp[i-1][j]*(1-p[i]))%mod; } for(int i=0;i<=n;i++) cout<<(dp[n][i]+mod)%mod<<" "; return 0; }
D:数三角
输入
3
0 0
-1145 1
1 0输出
1- 判断是能不能构成，a+b!=c,我直接用叉积就不用开放了
- 不是钝三角:\(a^2+b^2<c^2\)，我用的是向量<0
#include <iostream> #include <cstring> #include <cstdio> using namespace std; struct point{ double x,y; }p[550]; int n,ans=0; bool dj(point a,point b,point c){ if((b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y)==0)return false; if((b.x-a.x)*(c.x-a.x)+(b.y-a.y)*(c.y-a.y)<0)return true; if((a.x-b.x)*(c.x-b.x)+(a.y-b.y)*(c.y-b.y)<0)return true; if((a.x-c.x)*(b.x-c.x)+(a.y-c.y)*(b.y-c.y)<0)return true; return false; } int main(){ scanf("%d",&n); for(int i=0;i<n;i++)cin>>p[i].x>>p[i].y; for(int i=0;i<n;i++){ for(int j=i+1;j<n;j++){ for(int k=j+1;k<n;k++){ if(dj(p[i],p[j],p[k]))ans++; } } } cout<<ans; return 0; }
E:做计数
等式同平方得到 \[i+j+2\sqrt{ij}=k\] \[\sqrt{ij}=\frac{k-i-j}{2}\] 那么要么\((k-i-j)/2=几.5\)或者\((k-i-j)/2=整数\) 但是如果\(\sqrt{ij}=几.5\)那么\(ij=几.25\)而\(ij \in \mathbb{N}\)，所以\(\sqrt{ij} \in \mathbb{N}\) 我们枚举\(\sqrt{ij}\)即可
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int n,ans=0;
int main(){
scanf("%d",&n);
for(int sij=1;sij*sij<=n;sij++){
int tmp=0,ij=sij*sij;
for(int i=1;i<=sij;i++)
if(ij%i==0)tmp++;
ans+=tmp*2-1;
}
cout<<ans;
}F：拿物品
输入
3
8 7 6
5 4 21 3
23 1
2
也会被判定为正确开始我想的是贪心： 作为一个人取东西有两个目的：
- 取东西的时候自己取的应该尽可能大
- 取得的东西应该防止对手拉开与自己尽可能大的距离
这两个就是矛盾的...
- 取东西的时候自己取的应该尽可能大的方法是取对自己大的
- 取得的东西应该防止对手拉开与自己尽可能大的距离的方法是取对别人最大的而对自己最小的
那是取最自己最大的还是最小的呢？ 如果是ACM你两个分开试一下就过来qwq 这两个如何交叉使用呢？用\(A^*\)算法来决策？我写不出来jduge函数
正解是这样的，假设： N为某情况牛牛的最终得分 M为某情况牛可乐的最终得分 我们让牛牛的一个物品i和牛可乐的物品j交换 那么这时候牛牛的得分就变为了\(N^{'}=N-a_i+a_j\) 牛可乐的得分就变为了\(M^{'}=M-b_j+b_i\) 牛牛想：如果可以通过交换差距那么应该有 \[N^{'}-M^{'}>N-M\] \[N-a_i+a_j-M+b_j-b_i>N-M\] \[a_j+b_j>a_i+b_i\] 所以对于牛牛来说要优选选择\(a_i+b_i\)最大的物品 同时对于牛可乐来说也要选择\(a_i+b_i\)最大的物品 这就简单了，排序然后一个一个取
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
struct thing{
int id,a,b;
bool operator <(const thing t){
return a+b>t.a+t.b;
}
}s[200050];
int n;
int main(){
scanf("%d",&n);
for(int i=0;i<n;i++)scanf("%d",&s[i].a);
for(int i=0;i<n;i++){
scanf("%d",&s[i].b);
s[i].id=i;
}
sort(s,s+n);
for(int i=0;i<n;i+=2)printf("%d ",s[i].id+1);
printf("\n");
for(int i=1;i<n;i+=2)printf("%d ",s[i].id+1);
return 0;
}G：判正误
输入
2
1 1 4 5 1 4 258
114514 1919810 1 2 3 4 1输出
Yes
No首先我们必须用快速幂 然后呢？没有mod 不可能达到，用double？ 稍稍一丁点误差就废了 如果有一个mod就好了 手动规定\(mod=10^9+7\) 然后就挂了 但是你一个项继续用这个mod就过了 用\(mod=10^9+8\)然后就过了？？ 玄学？ 这道题的正解是设置好几个mod，然后分别快速幂，有一个不行就false，全可以就认为true 那怎么设置呢？ 自己试 因为这是acm可以多次尝试 什么****题目
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
long long a,b,c,d,e,f,g,t;
long long p=1000000007;
long long pow_mod(long long a, long long b){//a的b次方求余p
long long ret = 1;
while(b){
if(b & 1) ret = (ret * a) % p;
a = (a * a) % p;
b >>= 1;
}
return ret;
}
int main(){
scanf("%lld",&t);
while (t--){
scanf("%lld%lld%lld%lld%lld%lld%lld",&a,&b,&c,&d,&e,&f,&g);
if(pow_mod(a,d)+pow_mod(b,e)==(g%p)-(pow_mod(c,f)%p))cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
return 0;
}H：施魔法
输入
4 2
8 7 114514 114513输出
2首先我们要对于所有的元素按照能量值排序 我的想法就是贪心，首先我们知道选的越少极差越小，不能跳过这个数选其他数，让后面的组选这一个 所以我们只需要每次抉择这组选几个，这么选呢？首先这个有后效性吧，一共选多少组也没有规定，也没有上界，\(IDA^*\)也不可以，于是想到以下式子 \[f_i=\min_{j \in[i,i-k+1]}\{f_{j-1}+a_i-a_j\}=\min_{j \in [1,i-k+1]}\{f_{j-1}-a_j\}+a_i\] \(f_i\)为前i个的最优解
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n,k,a[300050];
long long dp[300050];
int main(){
memset(dp,0x3f3f3f3f,sizeof(dp));
scanf("%d%d",&n,&k);
for(int i=0;i<n;i++)scanf("%d",&a[i]);
sort(a,a+n);
dp[k-1]=a[k-1]-a[0];
for(int i=k;i<n;i++)
dp[i]=min(dp[i-1]-a[i-1]+a[i],dp[i-k]+a[i]-a[i-k+1]);
cout<<dp[n-1];
return 0;
}I：建通道
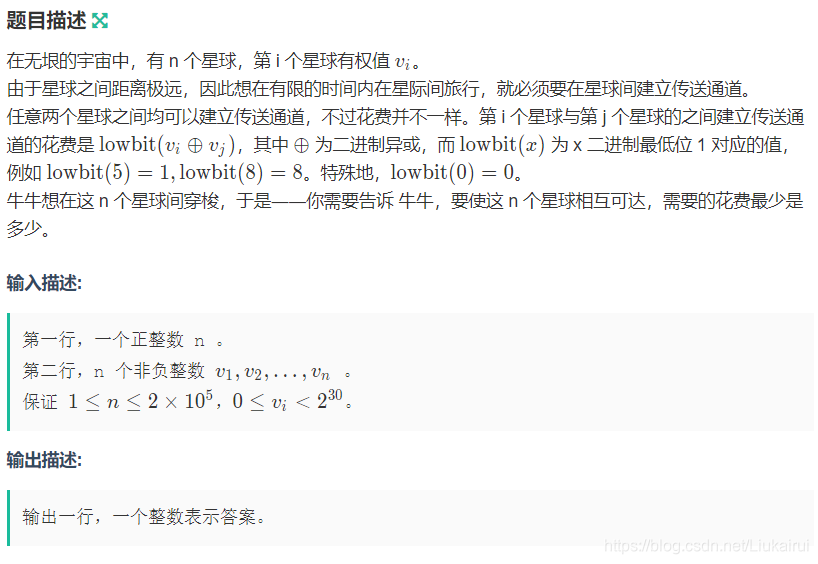输入
2
1 2输出
1首先按照经验来说，对于这种全联通图，如果把所有的边全写出来然后Prime跑一遍是肯定不行的，一定要耍点小聪明，于是我是这么想的，对于一个图，我们先把每个权值写出来，例如
000000
000010
001001
000001
000011
000001如果我排序一下
000000
000001
000001
000010
000011
001001000001
000001这两个点的权值为0 那直接去重，方便之后计算
000000
000001
000010
000011
001001#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAX_N=2e5+20;
long long n,m,v[MAX_N],ans=0;
int main(){
scanf("%lld",&n);
for(int i=0;i<n;i++)scanf("%lld",&v[i]);
sort(v,v+n);
m=unique(v,v+n)-v;
for(int i=1;i<m;i++){
long long x=v[i]^v[i-1];
ans+=(x&(-x));
}
printf("%lld",ans);
return 0;
}00000100
00100100
10000000一二的权值是32，但是一三权值是4 所以，我需要的是找到最低一位的1， 首先，我找到的是最低一位的1，所以之后位全是0！ 然后呢，对于所有这一位为0的，他们的与最低位1连接一定是权值最小的 写出代码，用|运算找出所有出现1的位然后找
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAX_N=2e5+20;
long long n,m,v[MAX_N],ans=0;
int main(){
scanf("%lld",&n);
for(int i=0;i<n;i++)scanf("%lld",&v[i]);
sort(v,v+n);
m=unique(v,v+n)-v;
long long tmp=v[0];
for(int i=1;i<m;i++)tmp|=v[i];
for(int i=0;(1<<i)<tmp;i++)
if((1<<i)&tmp){
cout<<((1<<i)*(m-1));
break;
}
return 0;
}还是挂了... 为啥，在上一思路的基础上，我们找到最小1的位置，然后讨论了0，但是我们没有讨论这一位为1的情况，例如
0000111101000
0000111111000
0000000100000找到的一定是第四位，所以一三链接一定是最好的，但是二呢，不是12而是二三...，还是无法定论，所以我们需要找到的是一个最低的1，并且这一位有的数是1有的数是0，我们只要随意让哪一位01相互匹配即可！ 这里用|找所有的1的位置，&找所有有0的位置 注意这里要特判答案为0，就是1个或0个星球
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAX_N=2e5+20;
long long n,m,v[MAX_N],ans=0;
int main(){
scanf("%lld",&n);
for(int i=0;i<n;i++)scanf("%lld",&v[i]);
sort(v,v+n);
m=unique(v,v+n)-v;
long long tmp1=v[0],tmp2=v[0];
for(int i=1;i<m;i++){tmp1|=v[i];tmp2&=v[i];}
if(m<=1){cout<<"0";return 0;}
for(int i=0;i<32;i++){
if(((1<<i)&tmp1)&&(!((1<<i)&tmp2))){
cout<<(1<<i)*(m-1);
break;
}
}
return 0;
}但是还有优化的空间，我们换一个顺序：要找的是一位，这一位有0,有1，然后再找到最小的哪一位 有0有1用异或，最小位lowbit即可
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAX_N=2e5+20;
long long n,m,v[MAX_N],ans=0;
int main(){
scanf("%lld",&n);
for(int i=0;i<n;i++)scanf("%lld",&v[i]);
sort(v,v+n);
m=unique(v,v+n)-v;
long long tmp1=v[0],tmp2=v[0];
for(int i=1;i<m;i++){tmp1|=v[i];tmp2&=v[i];}
long long r=tmp1^tmp2;
r=r&(-r);
cout<<(m-1)*r;
return 0;
}完成！ 最后请注意我们用位运算不要写 a&b==0 或者 a|b!=0 直接写 !(a&b) a|b 不知道为啥不这么写会挂，后补
J：求函数
示例 输入
2 3
1 1
1 0
1 2 114514 1919810
2 1 2
2 1 1输出
2148838
2先写下三项 \[ \begin{aligned} &f_l(1)=k_1+b_1\\ &f_{l+1}(f_l(1))=k_{l+1}k_l+k_{l+1}b_1+b_2 \\ &f_{l+2}(f_{l+1}(f_l(1)))=k_{l+2}k_{l+1}k_l+k_{l+2}k_{l+1}b_1+b_{l+2}b_2+b_3k_{l+1}k_l+b_3b_1k_{l+1}+b_3b_2 \end{aligned} \] 找下规律~ \[ f_r(f_{r-1}(\dots f_{l+1}(f_l(1))\dots ))=\prod\limits_{i=l}^{r}k_i+\sum\limits_{i=1}^{r}b_i\prod\limits_{j=i+1}^{r}k_j \]
由于涉及频繁修改与移动，我们采用线段树处理这个问题 维护两个线段树\(\prod\limits_{i=l}^{r}k_i\)与\(\sum\limits_{i=1}^{r}b_i\prod\limits_{j=i+1}^{r}k_j\) 第一个很好维护，第二个的合并较为复杂 \(\prod\limits_{i=l_1}^{r_1}k_i=n_1\),\(\prod\limits_{i=l_2}^{r_2}k_i=n_2\) \(\sum\limits_{i=l_1}^{r_1}b_i\prod\limits_{j=i+1}^{r}k_j=m_1\),\(\sum\limits_{i=l_2}^{r_2}b_i\prod\limits_{j=i+1}^{r}k_j=m_2\) \(\sum b_i\prod k_j=m_1*n_2+m_2\) 写出代码(注意这里由于第二个树合并不是一个简单地相加，我们只好修改了query函数的查询顺序，以往是有一个加一个，现在要分类讨论一下)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define LC (p<<1)
#define RC (LC|1)
#define M ((l+r)>>1)
#define mod 1000000007
#define MAX_N 200050
using namespace std;
typedef pair<long long,long long> PII;
long long s1[MAX_N<<2],s2[MAX_N<<2],k[MAX_N];
int n,m;
void up(int p){
s1[p]=(s1[LC]*s1[RC])%mod;
s2[p]=(s2[LC]*s1[RC]+s2[RC])%mod;
return;
}
void modify(int p,int x,int k,int b,int l,int r){
if(l==r){
s1[p]=k;
s2[p]=b;
return;
}
if(x<=M)modify(LC,x,k,b,l,M);
if(x>M)modify(RC,x,k,b,M+1,r);
up(p);
return;
}
PII query(int p,int x,int y,int l,int r){
if(x<=l&&r<=y)return make_pair(s1[p],s2[p]);
if(x<=M && y>M){
PII tmp1=query(LC,x,y,l,M),tmp2=query(RC,x,y,M+1,r);
return make_pair((tmp1.first*tmp2.first)%mod,(tmp1.second*tmp2.first+tmp2.second)%mod);
}
if(x<=M)return query(LC,x,y,l,M);
if(y>M)return query(RC,x,y,M+1,r);
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%lld",&k[i]);
for(int i=1;i<=n;i++){
long long b;
scanf("%lld",&b);
modify(1,i,k[i],b,1,n);
}
while(m--){
int a,b,c,d;
scanf("%d%d%d",&a,&b,&c);
if(a==1){
scanf("%d",&d);
modify(1,b,c,d,1,n);
}
else{
PII s=query(1,b,c,1,n);
printf("%lld\n",(s.first+s.second)%mod);
}
}
return 0;
}